从红黑树中删除
在本教程中,您将学习如何从红黑树中删除节点。 此外,您还将找到在 C,C++ ,Java 和 Python 上对红黑树执行删除操作的工作示例。
红黑树是一种自平衡二叉搜索树,其中每个节点都包含一个额外的位,用于表示该节点的颜色,红色还是黑色。
阅读本文之前,请参考红黑树上的文章。
删除节点可能会也可能不会破坏红黑树的红黑属性。 如果此操作违反了红黑色属性,则使用一种修复算法来重新获得红黑色属性。
从红黑树中删除元素
此操作从树中删除节点。 删除节点后,再次保留红黑属性。
-
令
nodeToBeDeleted为: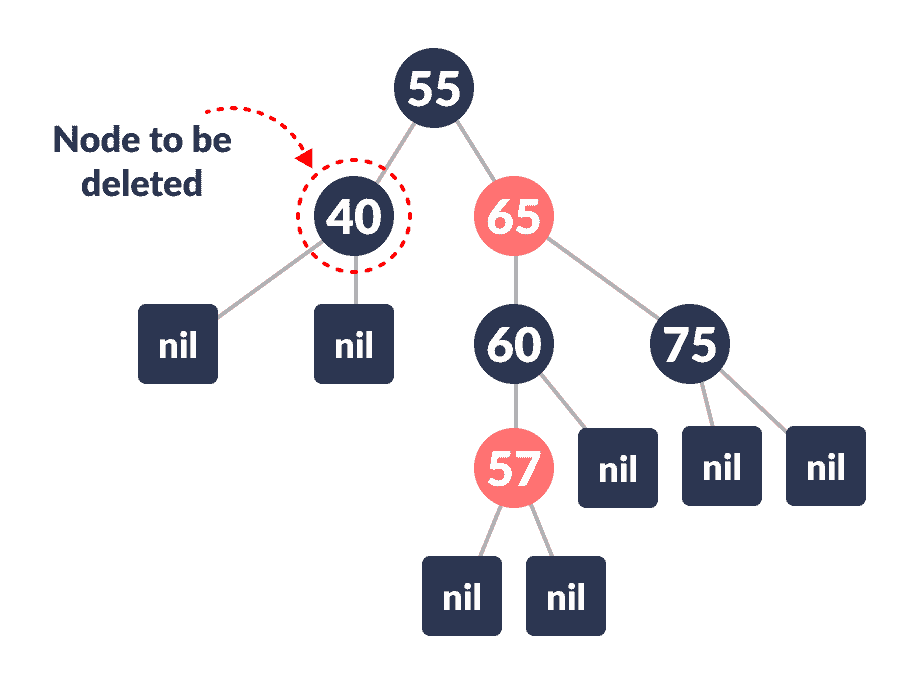
要删除的节点
-
将
nodeToBeDeleted的颜色保存在origrinalColor中。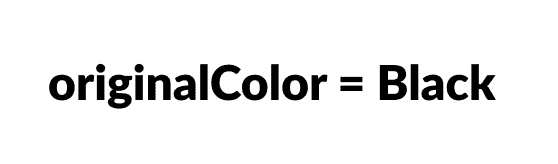
保存原始颜色
-
如果
nodeToBeDeleted的左子级是NULL-
将
nodeToBeDeleted的右子代分配给x。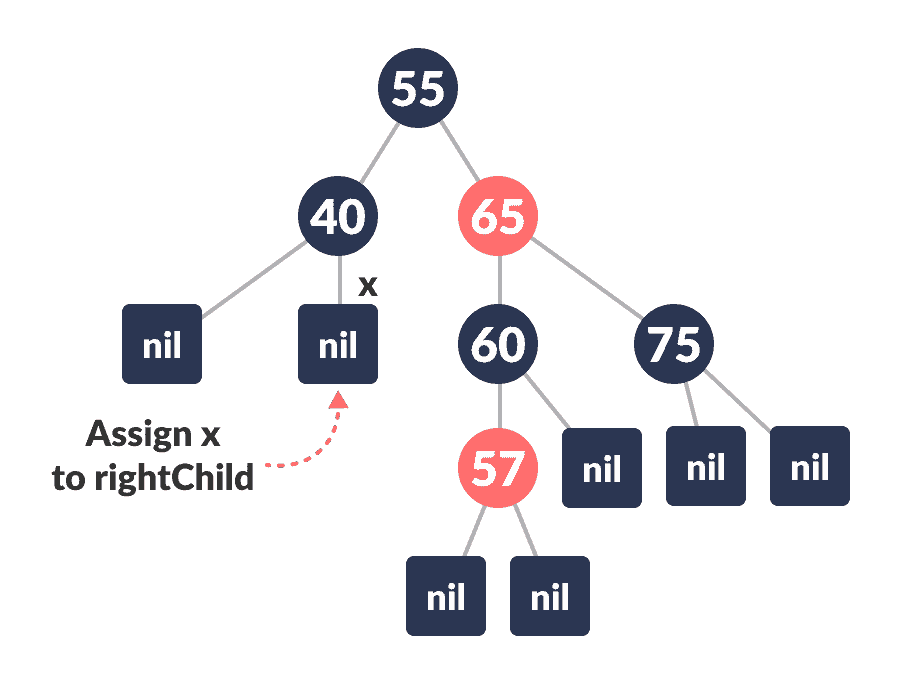
将
x分配给rightChild -
用
x移植nodeToBeDeleted。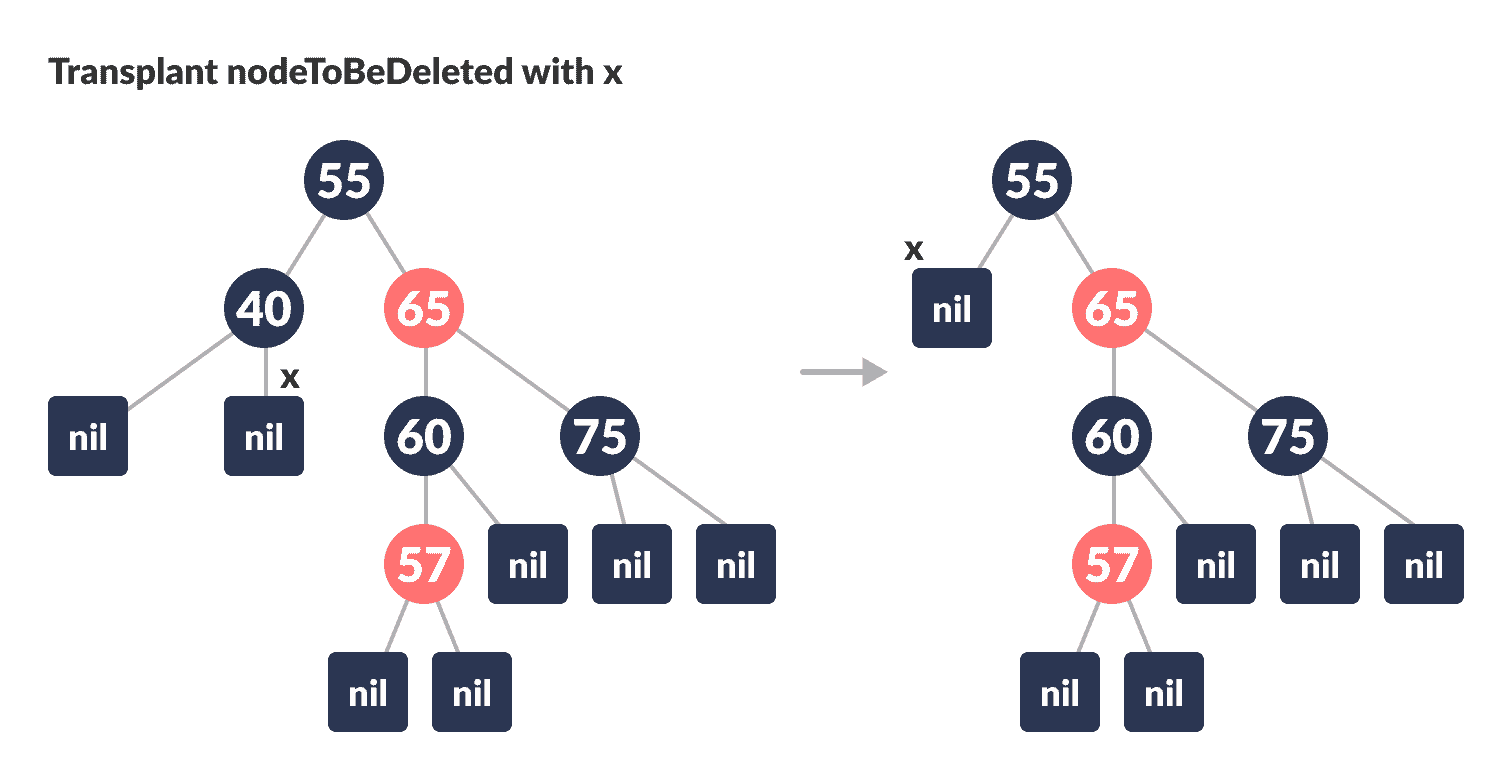
用
x移植nodeToBeDeleted
-
-
否则,如果
nodeToBeDeleted的右子对象是NULL- 将
nodeToBeDeleted的左子级分配到x中。 - 用
x移植nodeToBeDeleted。
- 将
-
否则
- 将
noteToBeDeleted的右子树的最小值分配到y中。 - 将
y的颜色保存在originalColor中。 - 将
y的rightChild分配到x中。 - 如果
y是nodeToBeDeleted的子级,则将x的父级设置为y。 - 否则,将
y移植为y的rightChild。 - 将
y移植到nodeToBeDeleted中。 - 使用
originalColor设置y的颜色。
- 将
-
如果
originalColor为黑色,则调用DeleteFix(x)。
删除后保持红黑属性的算法
当删除黑色节点时会执行此算法,因为它违反了红黑树的黑色深度属性。
通过假定节点x(占据y的原始位置)具有额外的黑色来纠正此冲突。 这使得节点x既不是红色的,也不是黑色的。 它是双黑色或黑色和红色。 这违反了红黑色属性。
但是,x的颜色属性未更改,而是在指向节点的x的表示中表示了额外的黑色。
如果多余的黑色可以去除
- 它到达根节点。
- 如果
x指向红黑节点。 在这种情况下,x被涂成黑色。 - 进行适当的旋转和重新着色。
以下算法保留了红黑树的属性。
-
执行以下操作,直到
x不是树的根并且x的颜色为黑色 -
如果
x是其父级的左子级,-
将
w分配给x的兄弟。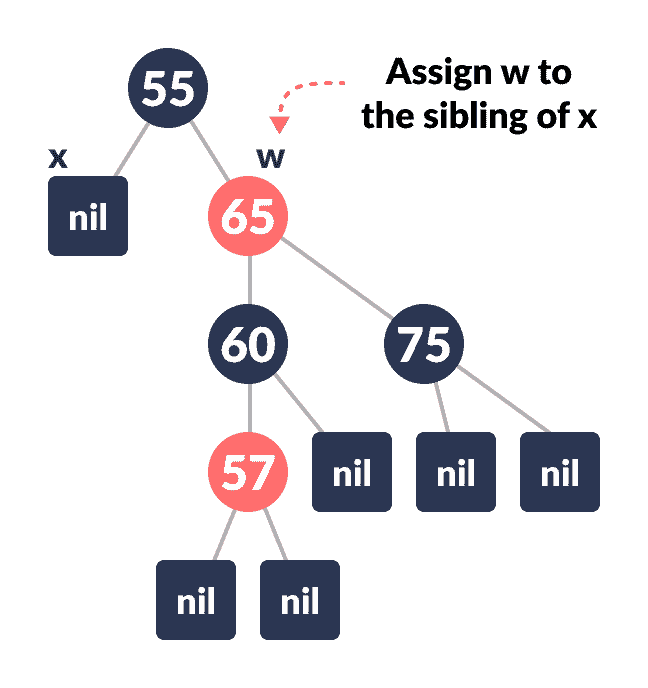
分配
w -
如果
x的同级是红色,则 情况 I:-
将
x的父级的右子级的颜色设置为黑色。 -
将
x的父级颜色设置为红色。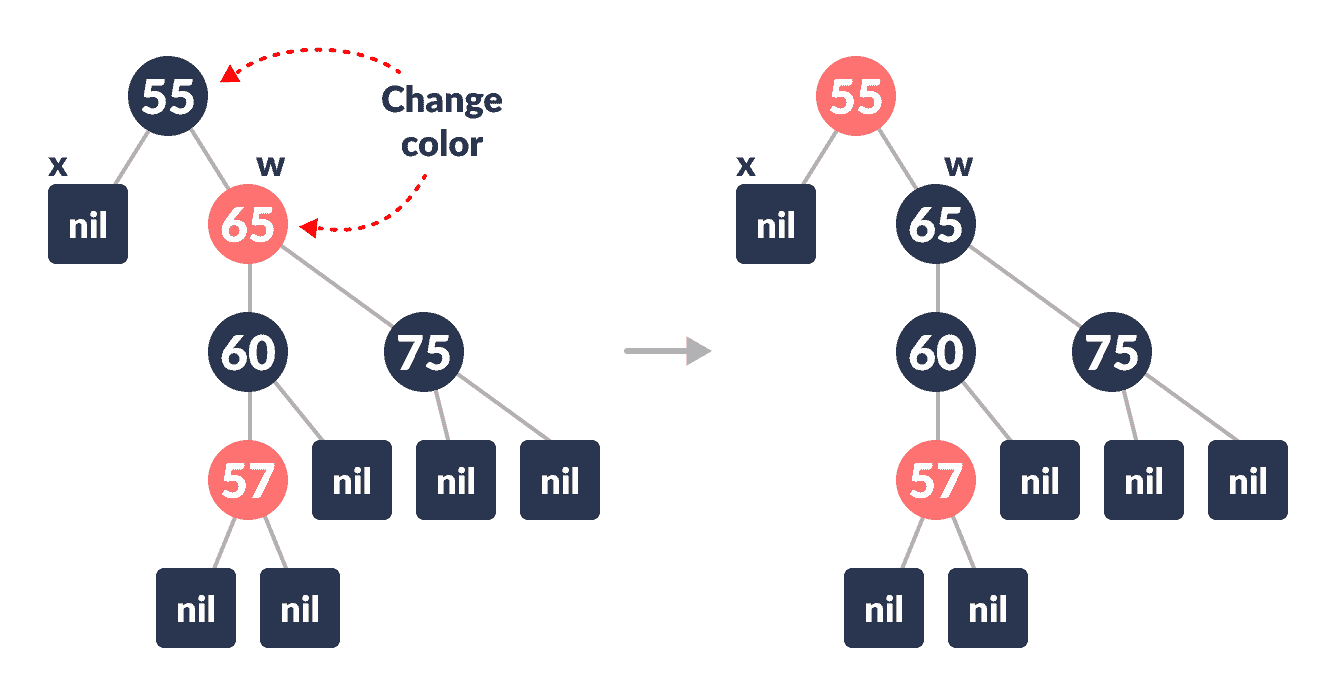
颜色更改
-
左旋转
x的父级。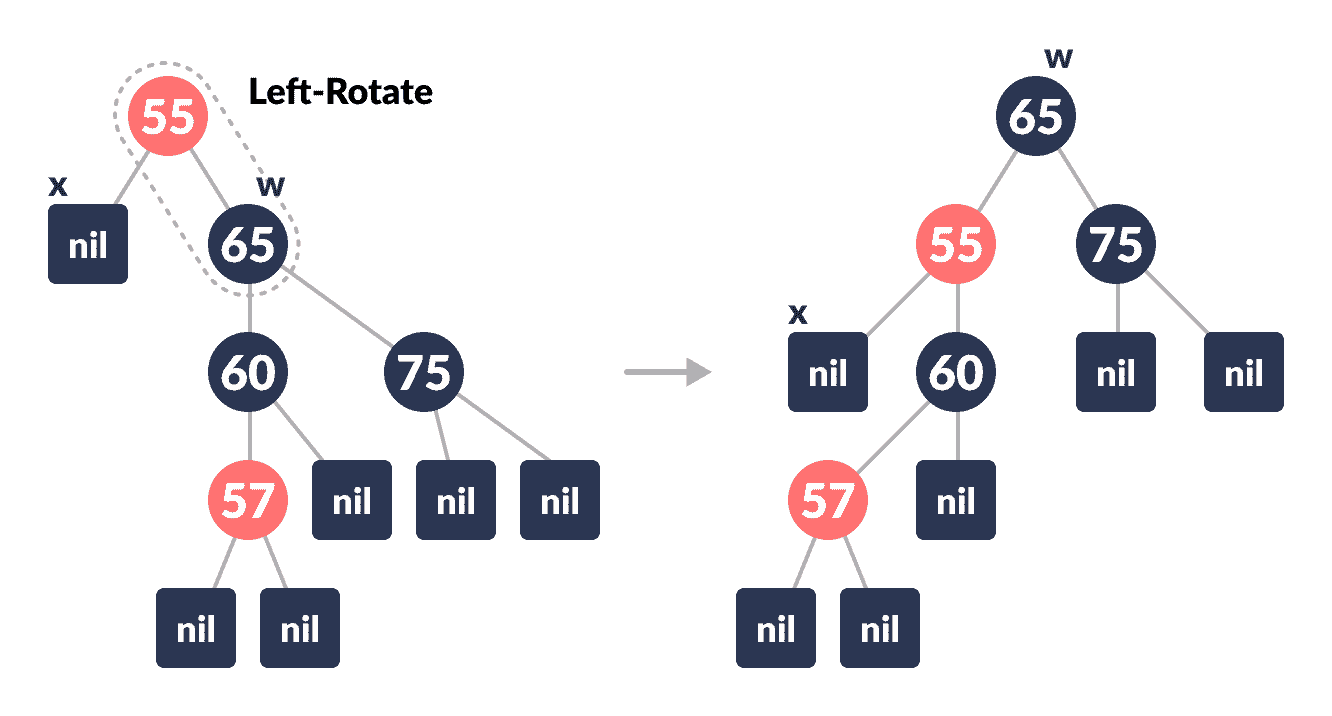
左旋
-
将
x的父级的rightChild分配给w。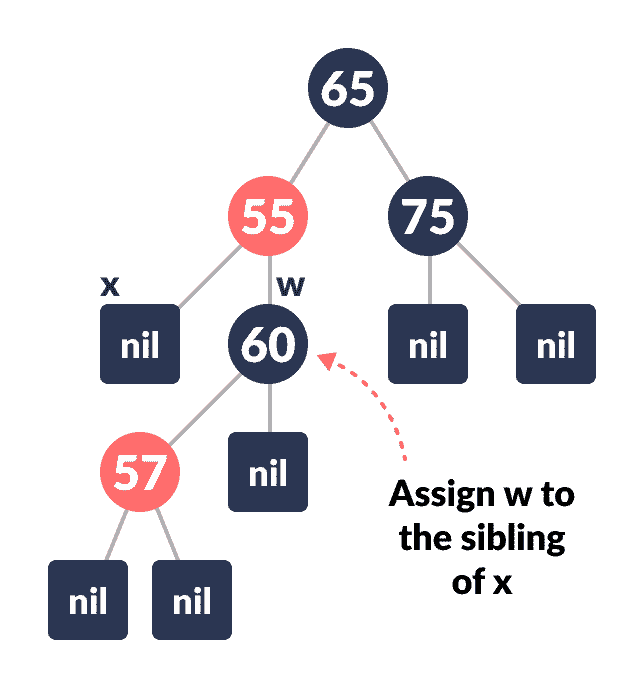
重新分配
-
-
如果
w的右侧和leftChild的颜色均为黑色,则 情况 II:- 将
w的颜色设置为红色 - 将
x的父级分配给x。
- 将
-
否则,如果
w的rightChild的颜色是黑色 情况 III:-
将
w的leftChild的颜色设置为黑色 -
将
w的颜色设置为红色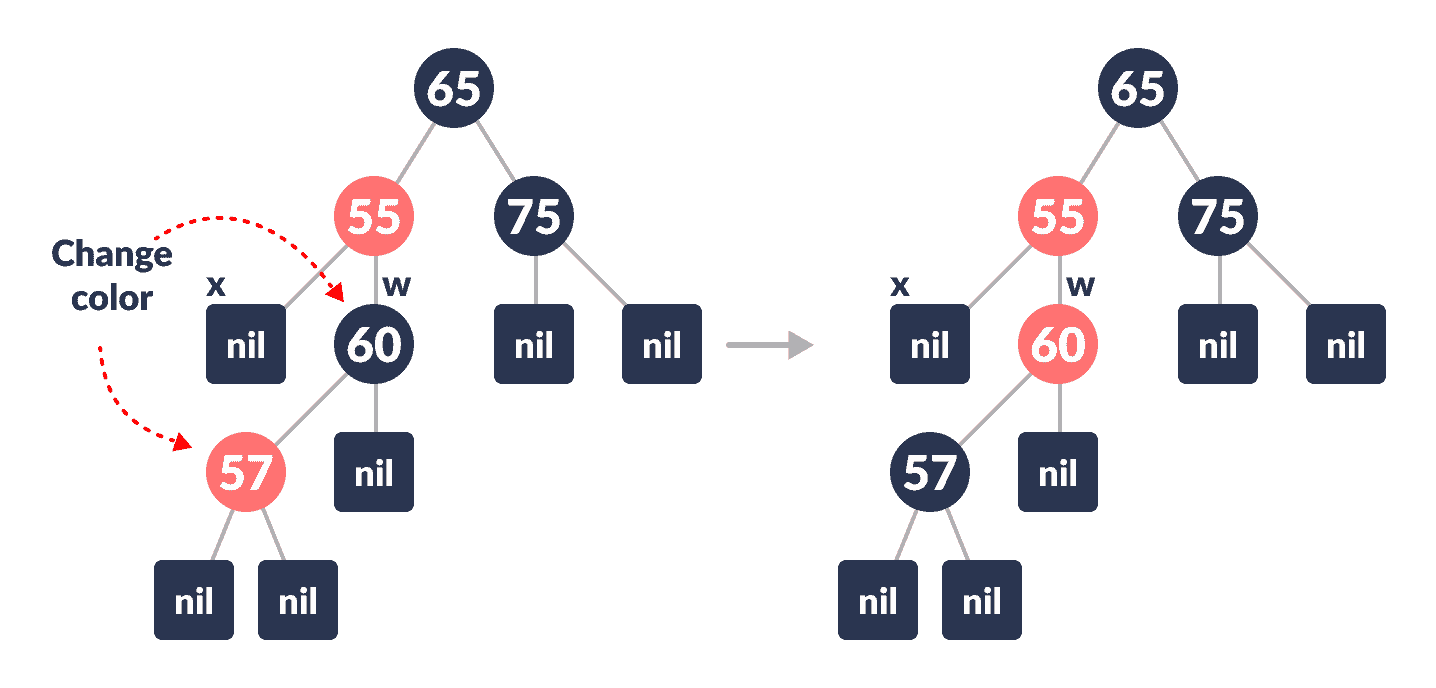
颜色更改
-
向右旋转
w。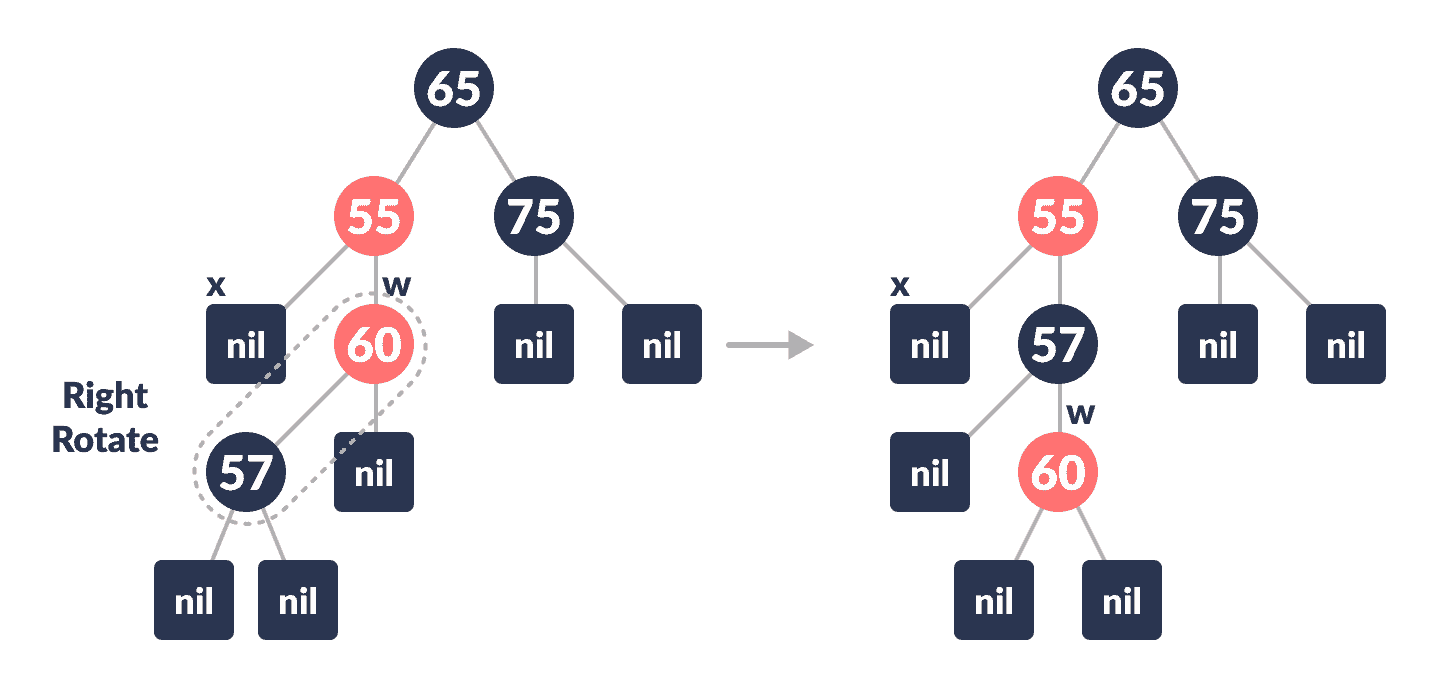
右旋
-
将
x的父级的rightChild分配给w。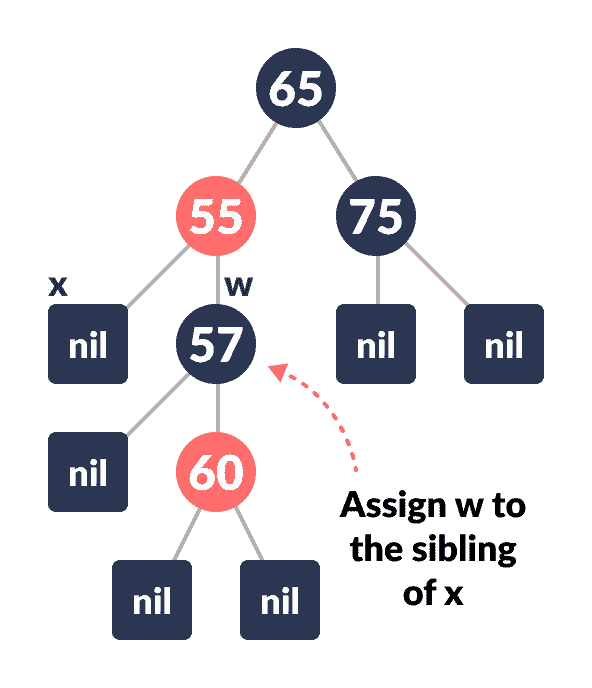
重新分配
-
-
如果以上情况均未发生,请执行以下操作。 情况 IV:
-
将
w的颜色设置为x的父代的颜色。 -
将
x的父级的父级颜色设置为黑色。 -
将
w的右子元素的颜色设置为黑色。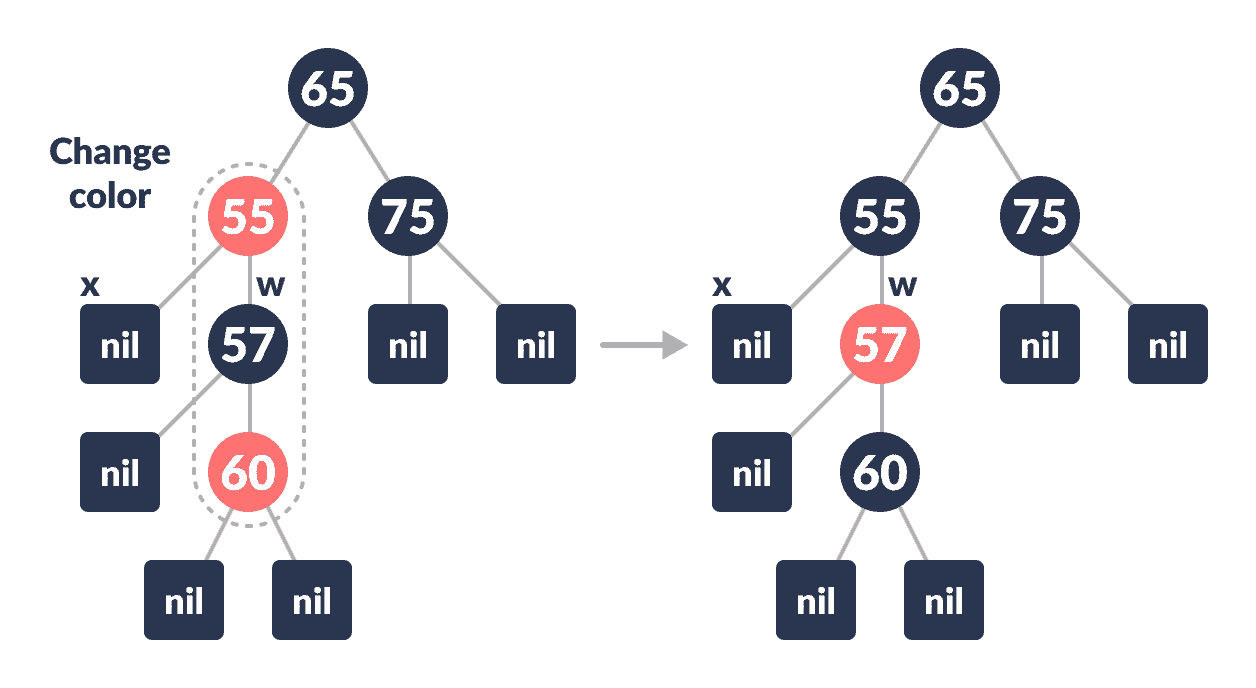
颜色更改
-
左旋转
x的父级。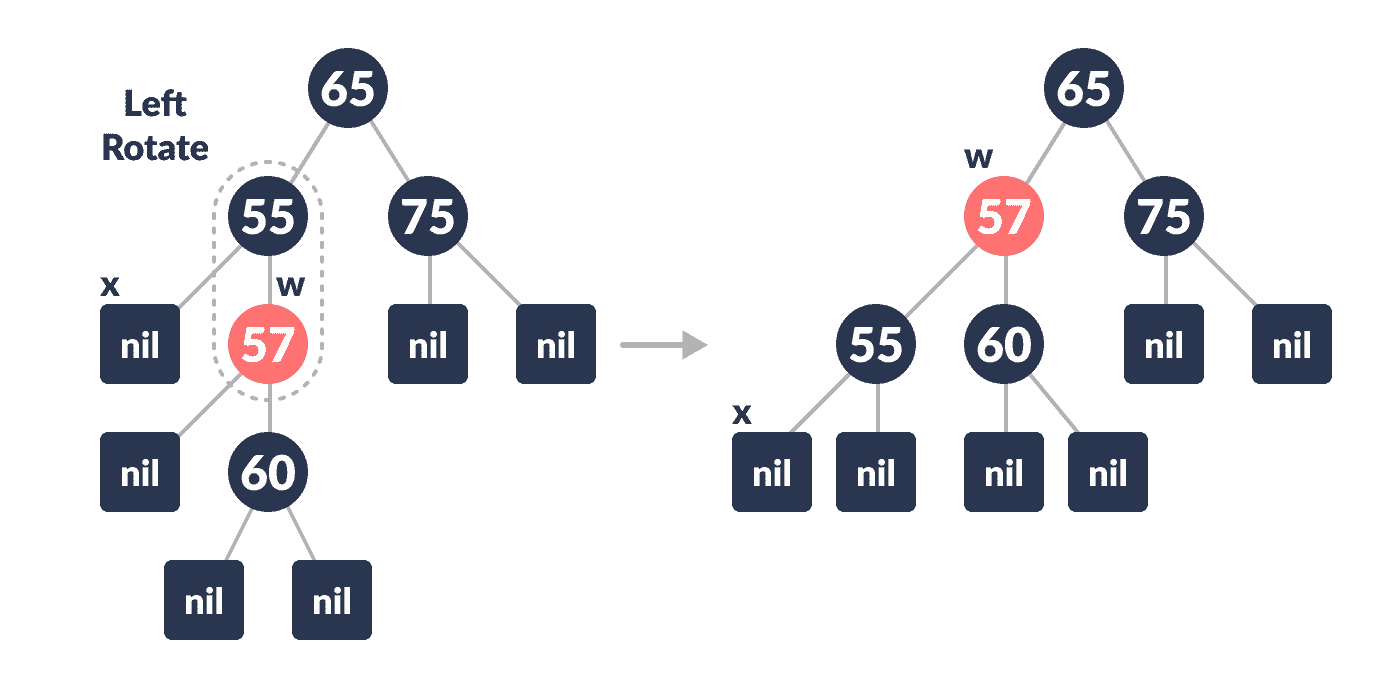
左旋
-
将
x设置为树的根。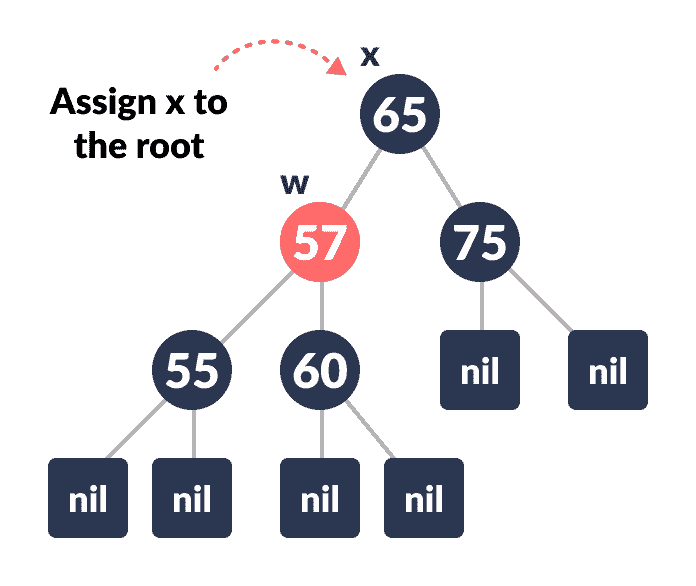
将
x设为根
-
-
-
其他与上面相同,将右侧更改为左侧,反之亦然。
-
将
x的颜色设置为黑色。
可以通过以下流程图了解上述情况的工作流程。
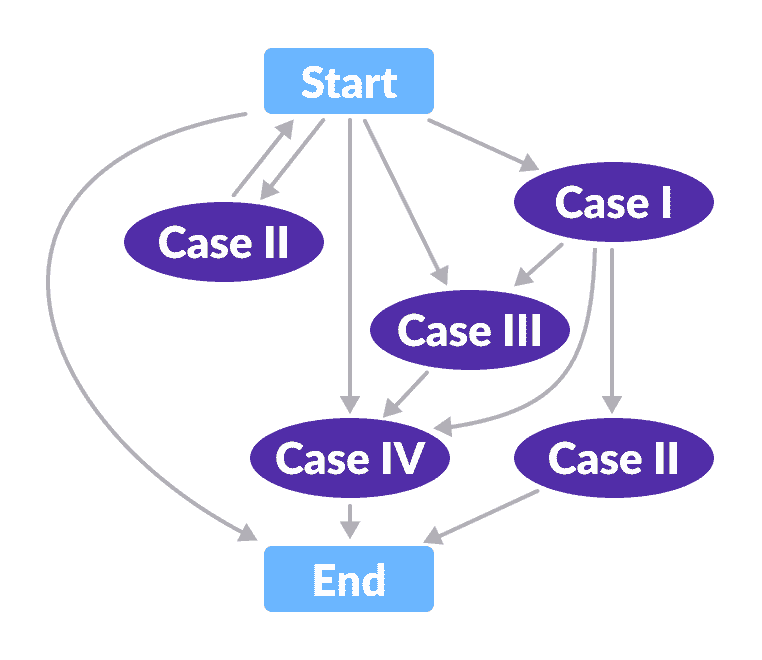
删除操作流程图
Python,Java 和 C/C++ 示例
# Implementing Red-Black Tree in Python import sys # Node creation class Node(): def __init__(self, item): self.item = item self.parent = None self.left = None self.right = None self.color = 1 class RedBlackTree(): def __init__(self): self.TNULL = Node(0) self.TNULL.color = 0 self.TNULL.left = None self.TNULL.right = None self.root = self.TNULL # Preorder def pre_order_helper(self, node): if node != TNULL: sys.stdout.write(node.item + " ") self.pre_order_helper(node.left) self.pre_order_helper(node.right) # Inorder def in_order_helper(self, node): if node != TNULL: self.in_order_helper(node.left) sys.stdout.write(node.item + " ") self.in_order_helper(node.right) # Postorder def post_order_helper(self, node): if node != TNULL: self.post_order_helper(node.left) self.post_order_helper(node.right) sys.stdout.write(node.item + " ") # Search the tree def search_tree_helper(self, node, key): if node == TNULL or key == node.item: return node if key < node.item: return self.search_tree_helper(node.left, key) return self.search_tree_helper(node.right, key) # Balancing the tree after deletion def delete_fix(self, x): while x != self.root and x.color == 0: if x == x.parent.left: s = x.parent.right if s.color == 1: s.color = 0 x.parent.color = 1 self.left_rotate(x.parent) s = x.parent.right if s.left.color == 0 and s.right.color == 0: s.color = 1 x = x.parent else: if s.right.color == 0: s.left.color = 0 s.color = 1 self.right_rotate(s) s = x.parent.right s.color = x.parent.color x.parent.color = 0 s.right.color = 0 self.left_rotate(x.parent) x = self.root else: s = x.parent.left if s.color == 1: s.color = 0 x.parent.color = 1 self.right_rotate(x.parent) s = x.parent.left if s.right.color == 0 and s.right.color == 0: s.color = 1 x = x.parent else: if s.left.color == 0: s.right.color = 0 s.color = 1 self.left_rotate(s) s = x.parent.left s.color = x.parent.color x.parent.color = 0 s.left.color = 0 self.right_rotate(x.parent) x = self.root x.color = 0 def __rb_transplant(self, u, v): if u.parent == None: self.root = v elif u == u.parent.left: u.parent.left = v else: u.parent.right = v v.parent = u.parent # Node deletion def delete_node_helper(self, node, key): z = self.TNULL while node != self.TNULL: if node.item == key: z = node if node.item <= key: node = node.right else: node = node.left if z == self.TNULL: print("Cannot find key in the tree") return y = z y_original_color = y.color if z.left == self.TNULL: x = z.right self.__rb_transplant(z, z.right) elif (z.right == self.TNULL): x = z.left self.__rb_transplant(z, z.left) else: y = self.minimum(z.right) y_original_color = y.color x = y.right if y.parent == z: x.parent = y else: self.__rb_transplant(y, y.right) y.right = z.right y.right.parent = y self.__rb_transplant(z, y) y.left = z.left y.left.parent = y y.color = z.color if y_original_color == 0: self.delete_fix(x) # Balance the tree after insertion def fix_insert(self, k): while k.parent.color == 1: if k.parent == k.parent.parent.right: u = k.parent.parent.left if u.color == 1: u.color = 0 k.parent.color = 0 k.parent.parent.color = 1 k = k.parent.parent else: if k == k.parent.left: k = k.parent self.right_rotate(k) k.parent.color = 0 k.parent.parent.color = 1 self.left_rotate(k.parent.parent) else: u = k.parent.parent.right if u.color == 1: u.color = 0 k.parent.color = 0 k.parent.parent.color = 1 k = k.parent.parent else: if k == k.parent.right: k = k.parent self.left_rotate(k) k.parent.color = 0 k.parent.parent.color = 1 self.right_rotate(k.parent.parent) if k == self.root: break self.root.color = 0 # Printing the tree def __print_helper(self, node, indent, last): if node != self.TNULL: sys.stdout.write(indent) if last: sys.stdout.write("R----") indent += " " else: sys.stdout.write("L----") indent += "| " s_color = "RED" if node.color == 1 else "BLACK" print(str(node.item) + "(" + s_color + ")") self.__print_helper(node.left, indent, False) self.__print_helper(node.right, indent, True) def preorder(self): self.pre_order_helper(self.root) def inorder(self): self.in_order_helper(self.root) def postorder(self): self.post_order_helper(self.root) def searchTree(self, k): return self.search_tree_helper(self.root, k) def minimum(self, node): while node.left != self.TNULL: node = node.left return node def maximum(self, node): while node.right != self.TNULL: node = node.right return node def successor(self, x): if x.right != self.TNULL: return self.minimum(x.right) y = x.parent while y != self.TNULL and x == y.right: x = y y = y.parent return y def predecessor(self, x): if (x.left != self.TNULL): return self.maximum(x.left) y = x.parent while y != self.TNULL and x == y.left: x = y y = y.parent return y def left_rotate(self, x): y = x.right x.right = y.left if y.left != self.TNULL: y.left.parent = x y.parent = x.parent if x.parent == None: self.root = y elif x == x.parent.left: x.parent.left = y else: x.parent.right = y y.left = x x.parent = y def right_rotate(self, x): y = x.left x.left = y.right if y.right != self.TNULL: y.right.parent = x y.parent = x.parent if x.parent == None: self.root = y elif x == x.parent.right: x.parent.right = y else: x.parent.left = y y.right = x x.parent = y def insert(self, key): node = Node(key) node.parent = None node.item = key node.left = self.TNULL node.right = self.TNULL node.color = 1 y = None x = self.root while x != self.TNULL: y = x if node.item < x.item: x = x.left else: x = x.right node.parent = y if y == None: self.root = node elif node.item < y.item: y.left = node else: y.right = node if node.parent == None: node.color = 0 return if node.parent.parent == None: return self.fix_insert(node) def get_root(self): return self.root def delete_node(self, item): self.delete_node_helper(self.root, item) def print_tree(self): self.__print_helper(self.root, "", True) if __name__ == "__main__": bst = RedBlackTree() bst.insert(55) bst.insert(40) bst.insert(65) bst.insert(60) bst.insert(75) bst.insert(57) bst.print_tree() print("\nAfter deleting an element") bst.delete_node(40) bst.print_tree()
// Implementing Red-Black Tree in Java
class Node {
int data;
Node parent;
Node left;
Node right;
int color;
}
public class RedBlackTree {
private Node root;
private Node TNULL;
// Preorder
private void preOrderHelper(Node node) {
if (node != TNULL) {
System.out.print(node.data + " ");
preOrderHelper(node.left);
preOrderHelper(node.right);
}
}
// Inorder
private void inOrderHelper(Node node) {
if (node != TNULL) {
inOrderHelper(node.left);
System.out.print(node.data + " ");
inOrderHelper(node.right);
}
}
// Post order
private void postOrderHelper(Node node) {
if (node != TNULL) {
postOrderHelper(node.left);
postOrderHelper(node.right);
System.out.print(node.data + " ");
}
}
// Search the tree
private Node searchTreeHelper(Node node, int key) {
if (node == TNULL || key == node.data) {
return node;
}
if (key < node.data) {
return searchTreeHelper(node.left, key);
}
return searchTreeHelper(node.right, key);
}
// Balance the tree after deletion of a node
private void fixDelete(Node x) {
Node s;
while (x != root && x.color == 0) {
if (x == x.parent.left) {
s = x.parent.right;
if (s.color == 1) {
s.color = 0;
x.parent.color = 1;
leftRotate(x.parent);
s = x.parent.right;
}
if (s.left.color == 0 && s.right.color == 0) {
s.color = 1;
x = x.parent;
} else {
if (s.right.color == 0) {
s.left.color = 0;
s.color = 1;
rightRotate(s);
s = x.parent.right;
}
s.color = x.parent.color;
x.parent.color = 0;
s.right.color = 0;
leftRotate(x.parent);
x = root;
}
} else {
s = x.parent.left;
if (s.color == 1) {
s.color = 0;
x.parent.color = 1;
rightRotate(x.parent);
s = x.parent.left;
}
if (s.right.color == 0 && s.right.color == 0) {
s.color = 1;
x = x.parent;
} else {
if (s.left.color == 0) {
s.right.color = 0;
s.color = 1;
leftRotate(s);
s = x.parent.left;
}
s.color = x.parent.color;
x.parent.color = 0;
s.left.color = 0;
rightRotate(x.parent);
x = root;
}
}
}
x.color = 0;
}
private void rbTransplant(Node u, Node v) {
if (u.parent == null) {
root = v;
} else if (u == u.parent.left) {
u.parent.left = v;
} else {
u.parent.right = v;
}
v.parent = u.parent;
}
private void deleteNodeHelper(Node node, int key) {
Node z = TNULL;
Node x, y;
while (node != TNULL) {
if (node.data == key) {
z = node;
}
if (node.data <= key) {
node = node.right;
} else {
node = node.left;
}
}
if (z == TNULL) {
System.out.println("Couldn't find key in the tree");
return;
}
y = z;
int yOriginalColor = y.color;
if (z.left == TNULL) {
x = z.right;
rbTransplant(z, z.right);
} else if (z.right == TNULL) {
x = z.left;
rbTransplant(z, z.left);
} else {
y = minimum(z.right);
yOriginalColor = y.color;
x = y.right;
if (y.parent == z) {
x.parent = y;
} else {
rbTransplant(y, y.right);
y.right = z.right;
y.right.parent = y;
}
rbTransplant(z, y);
y.left = z.left;
y.left.parent = y;
y.color = z.color;
}
if (yOriginalColor == 0) {
fixDelete(x);
}
}
// Balance the node after insertion
private void fixInsert(Node k) {
Node u;
while (k.parent.color == 1) {
if (k.parent == k.parent.parent.right) {
u = k.parent.parent.left;
if (u.color == 1) {
u.color = 0;
k.parent.color = 0;
k.parent.parent.color = 1;
k = k.parent.parent;
} else {
if (k == k.parent.left) {
k = k.parent;
rightRotate(k);
}
k.parent.color = 0;
k.parent.parent.color = 1;
leftRotate(k.parent.parent);
}
} else {
u = k.parent.parent.right;
if (u.color == 1) {
u.color = 0;
k.parent.color = 0;
k.parent.parent.color = 1;
k = k.parent.parent;
} else {
if (k == k.parent.right) {
k = k.parent;
leftRotate(k);
}
k.parent.color = 0;
k.parent.parent.color = 1;
rightRotate(k.parent.parent);
}
}
if (k == root) {
break;
}
}
root.color = 0;
}
private void printHelper(Node root, String indent, boolean last) {
if (root != TNULL) {
System.out.print(indent);
if (last) {
System.out.print("R----");
indent += " ";
} else {
System.out.print("L----");
indent += "| ";
}
String sColor = root.color == 1 ? "RED" : "BLACK";
System.out.println(root.data + "(" + sColor + ")");
printHelper(root.left, indent, false);
printHelper(root.right, indent, true);
}
}
public RedBlackTree() {
TNULL = new Node();
TNULL.color = 0;
TNULL.left = null;
TNULL.right = null;
root = TNULL;
}
public void preorder() {
preOrderHelper(this.root);
}
public void inorder() {
inOrderHelper(this.root);
}
public void postorder() {
postOrderHelper(this.root);
}
public Node searchTree(int k) {
return searchTreeHelper(this.root, k);
}
public Node minimum(Node node) {
while (node.left != TNULL) {
node = node.left;
}
return node;
}
public Node maximum(Node node) {
while (node.right != TNULL) {
node = node.right;
}
return node;
}
public Node successor(Node x) {
if (x.right != TNULL) {
return minimum(x.right);
}
Node y = x.parent;
while (y != TNULL && x == y.right) {
x = y;
y = y.parent;
}
return y;
}
public Node predecessor(Node x) {
if (x.left != TNULL) {
return maximum(x.left);
}
Node y = x.parent;
while (y != TNULL && x == y.left) {
x = y;
y = y.parent;
}
return y;
}
public void leftRotate(Node x) {
Node y = x.right;
x.right = y.left;
if (y.left != TNULL) {
y.left.parent = x;
}
y.parent = x.parent;
if (x.parent == null) {
this.root = y;
} else if (x == x.parent.left) {
x.parent.left = y;
} else {
x.parent.right = y;
}
y.left = x;
x.parent = y;
}
public void rightRotate(Node x) {
Node y = x.left;
x.left = y.right;
if (y.right != TNULL) {
y.right.parent = x;
}
y.parent = x.parent;
if (x.parent == null) {
this.root = y;
} else if (x == x.parent.right) {
x.parent.right = y;
} else {
x.parent.left = y;
}
y.right = x;
x.parent = y;
}
public void insert(int key) {
Node node = new Node();
node.parent = null;
node.data = key;
node.left = TNULL;
node.right = TNULL;
node.color = 1;
Node y = null;
Node x = this.root;
while (x != TNULL) {
y = x;
if (node.data < x.data) {
x = x.left;
} else {
x = x.right;
}
}
node.parent = y;
if (y == null) {
root = node;
} else if (node.data < y.data) {
y.left = node;
} else {
y.right = node;
}
if (node.parent == null) {
node.color = 0;
return;
}
if (node.parent.parent == null) {
return;
}
fixInsert(node);
}
public Node getRoot() {
return this.root;
}
public void deleteNode(int data) {
deleteNodeHelper(this.root, data);
}
public void printTree() {
printHelper(this.root, "", true);
}
public static void main(String[] args) {
RedBlackTree bst = new RedBlackTree();
bst.insert(55);
bst.insert(40);
bst.insert(65);
bst.insert(60);
bst.insert(75);
bst.insert(57);
bst.printTree();
System.out.println("\nAfter deleting:");
bst.deleteNode(40);
bst.printTree();
}
}
// Implementing Red-Black Tree in C
#include <stdio.h>
#include <stdlib.h>
enum nodeColor {
RED,
BLACK
};
struct rbNode {
int data, color;
struct rbNode *link[2];
};
struct rbNode *root = NULL;
// Create a red-black tree
struct rbNode *createNode(int data) {
struct rbNode *newnode;
newnode = (struct rbNode *)malloc(sizeof(struct rbNode));
newnode->data = data;
newnode->color = RED;
newnode->link[0] = newnode->link[1] = NULL;
return newnode;
}
// Insert an node
void insertion(int data) {
struct rbNode *stack[98], *ptr, *newnode, *xPtr, *yPtr;
int dir[98], ht = 0, index;
ptr = root;
if (!root) {
root = createNode(data);
return;
}
stack[ht] = root;
dir[ht++] = 0;
while (ptr != NULL) {
if (ptr->data == data) {
printf("Duplicates Not Allowed!!\n");
return;
}
index = (data - ptr->data) > 0 ? 1 : 0;
stack[ht] = ptr;
ptr = ptr->link[index];
dir[ht++] = index;
}
stack[ht - 1]->link[index] = newnode = createNode(data);
while ((ht >= 3) && (stack[ht - 1]->color == RED)) {
if (dir[ht - 2] == 0) {
yPtr = stack[ht - 2]->link[1];
if (yPtr != NULL && yPtr->color == RED) {
stack[ht - 2]->color = RED;
stack[ht - 1]->color = yPtr->color = BLACK;
ht = ht - 2;
} else {
if (dir[ht - 1] == 0) {
yPtr = stack[ht - 1];
} else {
xPtr = stack[ht - 1];
yPtr = xPtr->link[1];
xPtr->link[1] = yPtr->link[0];
yPtr->link[0] = xPtr;
stack[ht - 2]->link[0] = yPtr;
}
xPtr = stack[ht - 2];
xPtr->color = RED;
yPtr->color = BLACK;
xPtr->link[0] = yPtr->link[1];
yPtr->link[1] = xPtr;
if (xPtr == root) {
root = yPtr;
} else {
stack[ht - 3]->link[dir[ht - 3]] = yPtr;
}
break;
}
} else {
yPtr = stack[ht - 2]->link[0];
if ((yPtr != NULL) && (yPtr->color == RED)) {
stack[ht - 2]->color = RED;
stack[ht - 1]->color = yPtr->color = BLACK;
ht = ht - 2;
} else {
if (dir[ht - 1] == 1) {
yPtr = stack[ht - 1];
} else {
xPtr = stack[ht - 1];
yPtr = xPtr->link[0];
xPtr->link[0] = yPtr->link[1];
yPtr->link[1] = xPtr;
stack[ht - 2]->link[1] = yPtr;
}
xPtr = stack[ht - 2];
yPtr->color = BLACK;
xPtr->color = RED;
xPtr->link[1] = yPtr->link[0];
yPtr->link[0] = xPtr;
if (xPtr == root) {
root = yPtr;
} else {
stack[ht - 3]->link[dir[ht - 3]] = yPtr;
}
break;
}
}
}
root->color = BLACK;
}
// Delete a node
void deletion(int data) {
struct rbNode *stack[98], *ptr, *xPtr, *yPtr;
struct rbNode *pPtr, *qPtr, *rPtr;
int dir[98], ht = 0, diff, i;
enum nodeColor color;
if (!root) {
printf("Tree not available\n");
return;
}
ptr = root;
while (ptr != NULL) {
if ((data - ptr->data) == 0)
break;
diff = (data - ptr->data) > 0 ? 1 : 0;
stack[ht] = ptr;
dir[ht++] = diff;
ptr = ptr->link[diff];
}
if (ptr->link[1] == NULL) {
if ((ptr == root) && (ptr->link[0] == NULL)) {
free(ptr);
root = NULL;
} else if (ptr == root) {
root = ptr->link[0];
free(ptr);
} else {
stack[ht - 1]->link[dir[ht - 1]] = ptr->link[0];
}
} else {
xPtr = ptr->link[1];
if (xPtr->link[0] == NULL) {
xPtr->link[0] = ptr->link[0];
color = xPtr->color;
xPtr->color = ptr->color;
ptr->color = color;
if (ptr == root) {
root = xPtr;
} else {
stack[ht - 1]->link[dir[ht - 1]] = xPtr;
}
dir[ht] = 1;
stack[ht++] = xPtr;
} else {
i = ht++;
while (1) {
dir[ht] = 0;
stack[ht++] = xPtr;
yPtr = xPtr->link[0];
if (!yPtr->link[0])
break;
xPtr = yPtr;
}
dir[i] = 1;
stack[i] = yPtr;
if (i > 0)
stack[i - 1]->link[dir[i - 1]] = yPtr;
yPtr->link[0] = ptr->link[0];
xPtr->link[0] = yPtr->link[1];
yPtr->link[1] = ptr->link[1];
if (ptr == root) {
root = yPtr;
}
color = yPtr->color;
yPtr->color = ptr->color;
ptr->color = color;
}
}
if (ht < 1)
return;
if (ptr->color == BLACK) {
while (1) {
pPtr = stack[ht - 1]->link[dir[ht - 1]];
if (pPtr && pPtr->color == RED) {
pPtr->color = BLACK;
break;
}
if (ht < 2)
break;
if (dir[ht - 2] == 0) {
rPtr = stack[ht - 1]->link[1];
if (!rPtr)
break;
if (rPtr->color == RED) {
stack[ht - 1]->color = RED;
rPtr->color = BLACK;
stack[ht - 1]->link[1] = rPtr->link[0];
rPtr->link[0] = stack[ht - 1];
if (stack[ht - 1] == root) {
root = rPtr;
} else {
stack[ht - 2]->link[dir[ht - 2]] = rPtr;
}
dir[ht] = 0;
stack[ht] = stack[ht - 1];
stack[ht - 1] = rPtr;
ht++;
rPtr = stack[ht - 1]->link[1];
}
if ((!rPtr->link[0] || rPtr->link[0]->color == BLACK) &&
(!rPtr->link[1] || rPtr->link[1]->color == BLACK)) {
rPtr->color = RED;
} else {
if (!rPtr->link[1] || rPtr->link[1]->color == BLACK) {
qPtr = rPtr->link[0];
rPtr->color = RED;
qPtr->color = BLACK;
rPtr->link[0] = qPtr->link[1];
qPtr->link[1] = rPtr;
rPtr = stack[ht - 1]->link[1] = qPtr;
}
rPtr->color = stack[ht - 1]->color;
stack[ht - 1]->color = BLACK;
rPtr->link[1]->color = BLACK;
stack[ht - 1]->link[1] = rPtr->link[0];
rPtr->link[0] = stack[ht - 1];
if (stack[ht - 1] == root) {
root = rPtr;
} else {
stack[ht - 2]->link[dir[ht - 2]] = rPtr;
}
break;
}
} else {
rPtr = stack[ht - 1]->link[0];
if (!rPtr)
break;
if (rPtr->color == RED) {
stack[ht - 1]->color = RED;
rPtr->color = BLACK;
stack[ht - 1]->link[0] = rPtr->link[1];
rPtr->link[1] = stack[ht - 1];
if (stack[ht - 1] == root) {
root = rPtr;
} else {
stack[ht - 2]->link[dir[ht - 2]] = rPtr;
}
dir[ht] = 1;
stack[ht] = stack[ht - 1];
stack[ht - 1] = rPtr;
ht++;
rPtr = stack[ht - 1]->link[0];
}
if ((!rPtr->link[0] || rPtr->link[0]->color == BLACK) &&
(!rPtr->link[1] || rPtr->link[1]->color == BLACK)) {
rPtr->color = RED;
} else {
if (!rPtr->link[0] || rPtr->link[0]->color == BLACK) {
qPtr = rPtr->link[1];
rPtr->color = RED;
qPtr->color = BLACK;
rPtr->link[1] = qPtr->link[0];
qPtr->link[0] = rPtr;
rPtr = stack[ht - 1]->link[0] = qPtr;
}
rPtr->color = stack[ht - 1]->color;
stack[ht - 1]->color = BLACK;
rPtr->link[0]->color = BLACK;
stack[ht - 1]->link[0] = rPtr->link[1];
rPtr->link[1] = stack[ht - 1];
if (stack[ht - 1] == root) {
root = rPtr;
} else {
stack[ht - 2]->link[dir[ht - 2]] = rPtr;
}
break;
}
}
ht--;
}
}
}
// Print the inorder traversal of the tree
void inorderTraversal(struct rbNode *node) {
if (node) {
inorderTraversal(node->link[0]);
printf("%d ", node->data);
inorderTraversal(node->link[1]);
}
return;
}
// Driver code
int main() {
int ch, data;
while (1) {
printf("1\. Insertion\t2\. Deletion\n");
printf("3\. Traverse\t4\. Exit");
printf("\nEnter your choice:");
scanf("%d", &ch);
switch (ch) {
case 1:
printf("Enter the element to insert:");
scanf("%d", &data);
insertion(data);
break;
case 2:
printf("Enter the element to delete:");
scanf("%d", &data);
deletion(data);
break;
case 3:
inorderTraversal(root);
printf("\n");
break;
case 4:
exit(0);
default:
printf("Not available\n");
break;
}
printf("\n");
}
return 0;
}
// Implementing Red-Black Tree in C++
#include <iostream>
using namespace std;
struct Node {
int data;
Node *parent;
Node *left;
Node *right;
int color;
};
typedef Node *NodePtr;
class RedBlackTree {
private:
NodePtr root;
NodePtr TNULL;
void initializeNULLNode(NodePtr node, NodePtr parent) {
node->data = 0;
node->parent = parent;
node->left = nullptr;
node->right = nullptr;
node->color = 0;
}
// Preorder
void preOrderHelper(NodePtr node) {
if (node != TNULL) {
cout << node->data << " ";
preOrderHelper(node->left);
preOrderHelper(node->right);
}
}
// Inorder
void inOrderHelper(NodePtr node) {
if (node != TNULL) {
inOrderHelper(node->left);
cout << node->data << " ";
inOrderHelper(node->right);
}
}
// Post order
void postOrderHelper(NodePtr node) {
if (node != TNULL) {
postOrderHelper(node->left);
postOrderHelper(node->right);
cout << node->data << " ";
}
}
NodePtr searchTreeHelper(NodePtr node, int key) {
if (node == TNULL || key == node->data) {
return node;
}
if (key < node->data) {
return searchTreeHelper(node->left, key);
}
return searchTreeHelper(node->right, key);
}
// For balancing the tree after deletion
void deleteFix(NodePtr x) {
NodePtr s;
while (x != root && x->color == 0) {
if (x == x->parent->left) {
s = x->parent->right;
if (s->color == 1) {
s->color = 0;
x->parent->color = 1;
leftRotate(x->parent);
s = x->parent->right;
}
if (s->left->color == 0 && s->right->color == 0) {
s->color = 1;
x = x->parent;
} else {
if (s->right->color == 0) {
s->left->color = 0;
s->color = 1;
rightRotate(s);
s = x->parent->right;
}
s->color = x->parent->color;
x->parent->color = 0;
s->right->color = 0;
leftRotate(x->parent);
x = root;
}
} else {
s = x->parent->left;
if (s->color == 1) {
s->color = 0;
x->parent->color = 1;
rightRotate(x->parent);
s = x->parent->left;
}
if (s->right->color == 0 && s->right->color == 0) {
s->color = 1;
x = x->parent;
} else {
if (s->left->color == 0) {
s->right->color = 0;
s->color = 1;
leftRotate(s);
s = x->parent->left;
}
s->color = x->parent->color;
x->parent->color = 0;
s->left->color = 0;
rightRotate(x->parent);
x = root;
}
}
}
x->color = 0;
}
void rbTransplant(NodePtr u, NodePtr v) {
if (u->parent == nullptr) {
root = v;
} else if (u == u->parent->left) {
u->parent->left = v;
} else {
u->parent->right = v;
}
v->parent = u->parent;
}
void deleteNodeHelper(NodePtr node, int key) {
NodePtr z = TNULL;
NodePtr x, y;
while (node != TNULL) {
if (node->data == key) {
z = node;
}
if (node->data <= key) {
node = node->right;
} else {
node = node->left;
}
}
if (z == TNULL) {
cout << "Key not found in the tree" << endl;
return;
}
y = z;
int y_original_color = y->color;
if (z->left == TNULL) {
x = z->right;
rbTransplant(z, z->right);
} else if (z->right == TNULL) {
x = z->left;
rbTransplant(z, z->left);
} else {
y = minimum(z->right);
y_original_color = y->color;
x = y->right;
if (y->parent == z) {
x->parent = y;
} else {
rbTransplant(y, y->right);
y->right = z->right;
y->right->parent = y;
}
rbTransplant(z, y);
y->left = z->left;
y->left->parent = y;
y->color = z->color;
}
delete z;
if (y_original_color == 0) {
deleteFix(x);
}
}
// For balancing the tree after insertion
void insertFix(NodePtr k) {
NodePtr u;
while (k->parent->color == 1) {
if (k->parent == k->parent->parent->right) {
u = k->parent->parent->left;
if (u->color == 1) {
u->color = 0;
k->parent->color = 0;
k->parent->parent->color = 1;
k = k->parent->parent;
} else {
if (k == k->parent->left) {
k = k->parent;
rightRotate(k);
}
k->parent->color = 0;
k->parent->parent->color = 1;
leftRotate(k->parent->parent);
}
} else {
u = k->parent->parent->right;
if (u->color == 1) {
u->color = 0;
k->parent->color = 0;
k->parent->parent->color = 1;
k = k->parent->parent;
} else {
if (k == k->parent->right) {
k = k->parent;
leftRotate(k);
}
k->parent->color = 0;
k->parent->parent->color = 1;
rightRotate(k->parent->parent);
}
}
if (k == root) {
break;
}
}
root->color = 0;
}
void printHelper(NodePtr root, string indent, bool last) {
if (root != TNULL) {
cout << indent;
if (last) {
cout << "R----";
indent += " ";
} else {
cout << "L----";
indent += "| ";
}
string sColor = root->color ? "RED" : "BLACK";
cout << root->data << "(" << sColor << ")" << endl;
printHelper(root->left, indent, false);
printHelper(root->right, indent, true);
}
}
public:
RedBlackTree() {
TNULL = new Node;
TNULL->color = 0;
TNULL->left = nullptr;
TNULL->right = nullptr;
root = TNULL;
}
void preorder() {
preOrderHelper(this->root);
}
void inorder() {
inOrderHelper(this->root);
}
void postorder() {
postOrderHelper(this->root);
}
NodePtr searchTree(int k) {
return searchTreeHelper(this->root, k);
}
NodePtr minimum(NodePtr node) {
while (node->left != TNULL) {
node = node->left;
}
return node;
}
NodePtr maximum(NodePtr node) {
while (node->right != TNULL) {
node = node->right;
}
return node;
}
NodePtr successor(NodePtr x) {
if (x->right != TNULL) {
return minimum(x->right);
}
NodePtr y = x->parent;
while (y != TNULL && x == y->right) {
x = y;
y = y->parent;
}
return y;
}
NodePtr predecessor(NodePtr x) {
if (x->left != TNULL) {
return maximum(x->left);
}
NodePtr y = x->parent;
while (y != TNULL && x == y->left) {
x = y;
y = y->parent;
}
return y;
}
void leftRotate(NodePtr x) {
NodePtr y = x->right;
x->right = y->left;
if (y->left != TNULL) {
y->left->parent = x;
}
y->parent = x->parent;
if (x->parent == nullptr) {
this->root = y;
} else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
void rightRotate(NodePtr x) {
NodePtr y = x->left;
x->left = y->right;
if (y->right != TNULL) {
y->right->parent = x;
}
y->parent = x->parent;
if (x->parent == nullptr) {
this->root = y;
} else if (x == x->parent->right) {
x->parent->right = y;
} else {
x->parent->left = y;
}
y->right = x;
x->parent = y;
}
// Inserting a node
void insert(int key) {
NodePtr node = new Node;
node->parent = nullptr;
node->data = key;
node->left = TNULL;
node->right = TNULL;
node->color = 1;
NodePtr y = nullptr;
NodePtr x = this->root;
while (x != TNULL) {
y = x;
if (node->data < x->data) {
x = x->left;
} else {
x = x->right;
}
}
node->parent = y;
if (y == nullptr) {
root = node;
} else if (node->data < y->data) {
y->left = node;
} else {
y->right = node;
}
if (node->parent == nullptr) {
node->color = 0;
return;
}
if (node->parent->parent == nullptr) {
return;
}
insertFix(node);
}
NodePtr getRoot() {
return this->root;
}
void deleteNode(int data) {
deleteNodeHelper(this->root, data);
}
void printTree() {
if (root) {
printHelper(this->root, "", true);
}
}
};
int main() {
RedBlackTree bst;
bst.insert(55);
bst.insert(40);
bst.insert(65);
bst.insert(60);
bst.insert(75);
bst.insert(57);
bst.printTree();
cout << endl
<< "After deleting" << endl;
bst.deleteNode(40);
bst.printTree();
}