堆数据结构

/heap-data-structure

在本教程中，您将学习什么是堆数据结构。 此外，您还将找到在 C，C++ ，Java 和 Python 中进行堆操作的工作示例。

堆数据结构是满足堆属性的完全二叉树，也称为二叉堆。

完全二叉树是一种特殊的二叉树，其中

• 除最后一个级别外，每个级别都已填充
• 所有节点都尽可能地向左

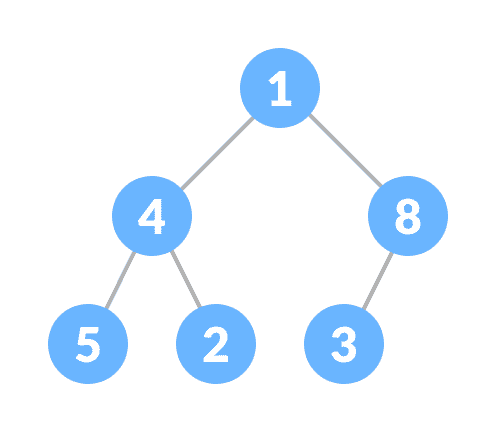
堆属性是其中节点的属性

• （对于最大堆）每个节点的键始终大于其子节点，并且根节点的键在所有其他节点中最大；
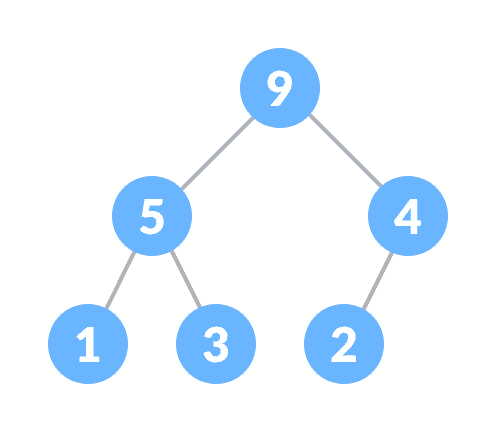
• （对于最小堆）每个节点的键始终小于子节点，而根节点的键在所有其他节点中最小。

堆操作

下面将对在堆上执行的一些重要操作及其算法进行描述。

建堆

建堆是从二叉树创建堆数据结构的过程。 它用于创建最小堆或最大堆。

1. 令输入数组为
2. 从数组创建完全二叉树
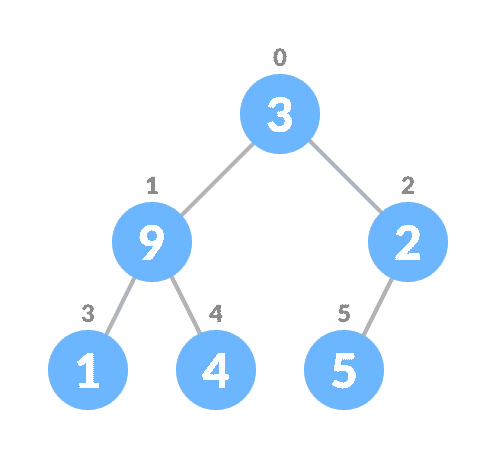
3. 从索引为n/2 - 1的非叶节点的第一个索引开始。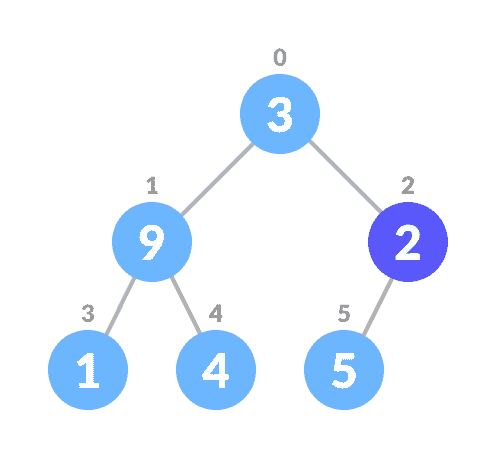
4. 将当前元素i设置为largest。
5. 左子索引由2i + 1给出，右子索引由2i + 2给出。 如果leftChild大于currentElement（即位于ith索引处的元素），则将leftChildIndex设置为最大。 如果rightChild大于largest中的元素，请将rightChildIndex设置为largest。
6. 将largest与currentElement交换
7. 重复步骤 3-7，直到子树也被堆积。

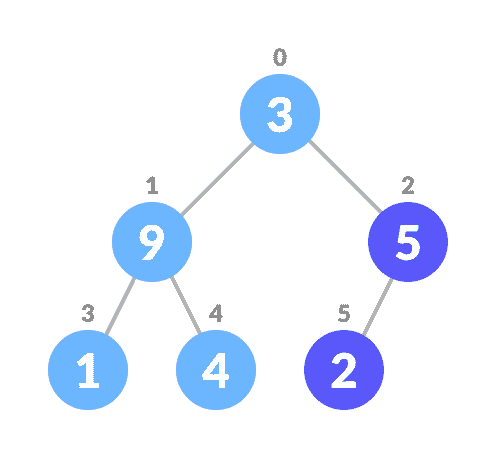
算法

Heapify(array, size, i)
  set i as largest
  leftChild = 2i + 1
  rightChild = 2i + 2

  if leftChild > array[largest]
    set leftChildIndex as largest
  if rightChild > array[largest]
    set rightChildIndex as largest

  swap array[i] and array[largest]

要创建最大堆：

MaxHeap(array, size)
  loop from the first index of non-leaf node down to zero
    call heapify

对于最小堆，对于所有节点，leftChild和rightChild都必须小于父节点。

将元素插入堆

最大堆中的插入算法

If there is no node, 
  create a newNode.
else (a node is already present)
  insert the newNode at the end (last node from left to right.)

heapify the array

1. 在树的末尾插入新元素。
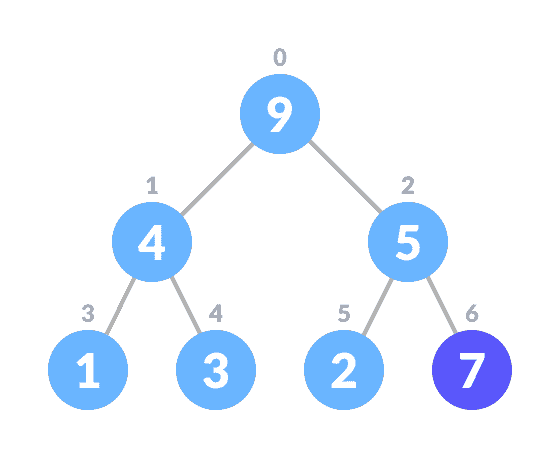
2. 对树建堆。

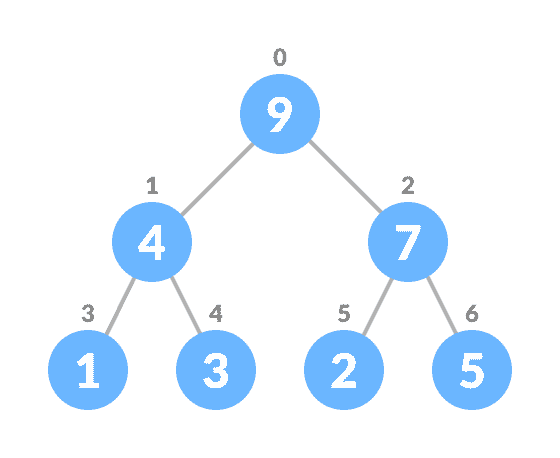
对于最小堆，对上述算法进行了修改，以使parentNode始终小于newNode。

从堆中删除元素

最大堆中的删除算法

If nodeToBeDeleted is the leafNode
  remove the node
Else swap nodeToBeDeleted with the lastLeafNode
  remove noteToBeDeleted

heapify the array

1. 选择要删除的元素。
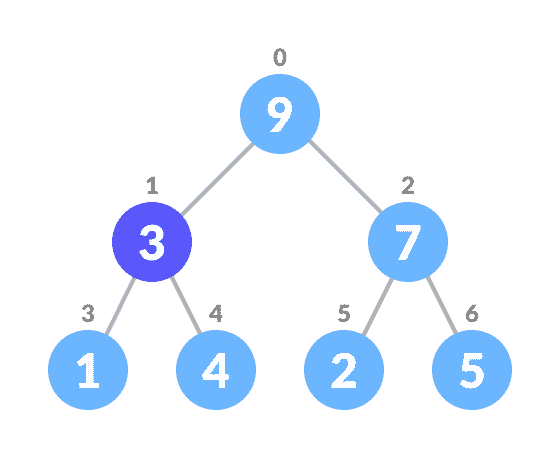
2. 将其与最后一个元素交换。
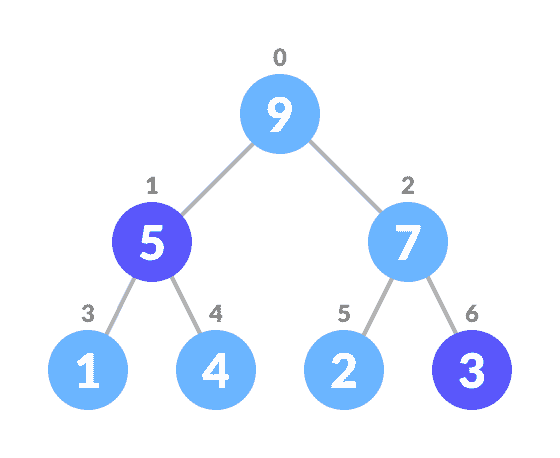
3. 删除最后一个元素。
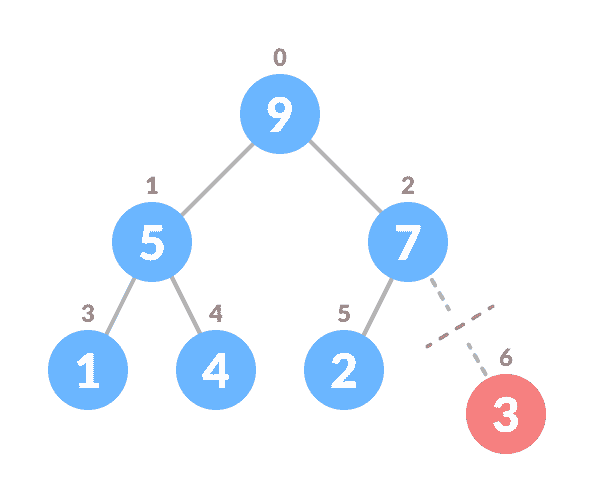
4. 对树建堆。

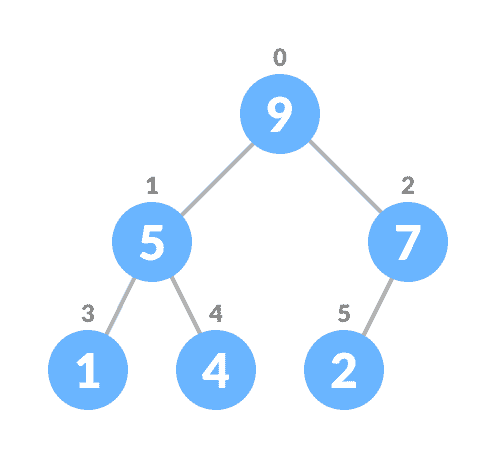
对于最小堆，对上述算法进行了修改，以使childNodes均小于currentNode。

窥视（找到最大/最小）

窥视操作从最大堆中返回最大元素，或者从最小堆中返回最小元素，而不删除节点。

对于最大堆和最小堆

return rootNode

提取最大/最小

从最大堆中删除后，Extract-Max返回具有最大值的节点，而从最小堆中删除后，Extract-Min返回具有最小值的节点。

Python，Java，C/C++ 示例

# Max-Heap data structure in Python

def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2 

    if l < n and arr[i] < arr[l]:
        largest = l

    if r < n and arr[largest] < arr[r]:
        largest = r

    if largest != i:
        arr[i],arr[largest] = arr[largest],arr[i]
        heapify(arr, n, largest)

def insert(array, newNum):
    size = len(array)
    if size == 0:
        array.append(newNum)
    else:
        array.append(newNum);
        for i in range((size//2)-1, -1, -1):
            heapify(array, size, i)

def deleteNode(array, num):
    size = len(array)
    i = 0
    for i in range(0, size):
        if num == array[i]:
            break

    array[i], array[size-1] = array[size-1], array[i]

    array.remove(size-1)

    for i in range((len(array)//2)-1, -1, -1):
        heapify(array, len(array), i)

arr = []

insert(arr, 3)
insert(arr, 4)
insert(arr, 9)
insert(arr, 5)
insert(arr, 2)

print ("Max-Heap array: " + str(arr))

deleteNode(arr, 4)
print("After deleting an element: " + str(arr)) 

 // Max-Heap data structure in Java

import java.util.ArrayList;

class Heap {
  void heapify(ArrayList<Integer> hT, int i) {
    int size = hT.size();
    int largest = i;
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    if (l < size && hT.get(l) > hT.get(largest))
      largest = l;
    if (r < size && hT.get(r) > hT.get(largest))
      largest = r;

    if (largest != i) {
      int temp = hT.get(largest);
      hT.set(largest, hT.get(i));
      hT.set(i, temp);

      heapify(hT, largest);
    }
  }

  void insert(ArrayList<Integer> hT, int newNum) {
    int size = hT.size();
    if (size == 0) {
      hT.add(newNum);
    } else {
      hT.add(newNum);
      for (int i = size / 2 - 1; i >= 0; i--) {
        heapify(hT, i);
      }
    }
  }

  void deleteNode(ArrayList<Integer> hT, int num)
  {
    int size = hT.size();
    int i;
    for (i = 0; i < size; i++)
    {
      if (num == hT.get(i))
        break;
    }

    int temp = hT.get(i);
    hT.set(i, hT.get(size-1));
    hT.set(size-1, temp);

    hT.remove(size-1);
    for (int j = size / 2 - 1; j >= 0; j--)
    {
      heapify(hT, j);
    }
  }

  void printArray(ArrayList<Integer> array, int size) {
    for (Integer i : array) {
      System.out.print(i + " ");
    }
    System.out.println();
  }

  public static void main(String args[]) {

    ArrayList<Integer> array = new ArrayList<Integer>();
    int size = array.size();

    Heap h = new Heap();
    h.insert(array, 3);
    h.insert(array, 4);
    h.insert(array, 9);
    h.insert(array, 5);
    h.insert(array, 2);

    System.out.println("Max-Heap array: ");
    h.printArray(array, size);

    h.deleteNode(array, 4);
    System.out.println("After deleting an element: ");
    h.printArray(array, size);
  }
}

// Max-Heap data structure in C

#include <stdio.h>
int size = 0;
void swap(int *a, int *b)
{
  int temp = *b;
  *b = *a;
  *a = temp;
}
void heapify(int array[], int size, int i)
{
  if (size == 1)
  {
    printf("Single element in the heap");
  }
  else
  {
    int largest = i;
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    if (l < size && array[l] > array[largest])
      largest = l;
    if (r < size && array[r] > array[largest])
      largest = r;
    if (largest != i)
    {
      swap(&array[i], &array[largest]);
      heapify(array, size, largest);
    }
  }
}
void insert(int array[], int newNum)
{
  if (size == 0)
  {
    array[0] = newNum;
    size += 1;
  }
  else
  {
    array[size] = newNum;
    size += 1;
    for (int i = size / 2 - 1; i >= 0; i--)
    {
      heapify(array, size, i);
    }
  }
}
void deleteRoot(int array[], int num)
{
  int i;
  for (i = 0; i < size; i++)
  {
    if (num == array[i])
      break;
  }

  swap(&array[i], &array[size - 1]);
  size -= 1;
  for (int i = size / 2 - 1; i >= 0; i--)
  {
    heapify(array, size, i);
  }
}
void printArray(int array[], int size)
{
  for (int i = 0; i < size; ++i)
    printf("%d ", array[i]);
  printf("\n");
}
int main()
{
  int array[10];

  insert(array, 3);
  insert(array, 4);
  insert(array, 9);
  insert(array, 5);
  insert(array, 2);

  printf("Max-Heap array: ");
  printArray(array, size);

  deleteRoot(array, 4);

  printf("After deleting an element: ");

  printArray(array, size);
}

// Max-Heap data structure in C++

#include <iostream>
#include <vector>
using namespace std;

void swap(int *a, int *b)
{
  int temp = *b;
  *b = *a;
  *a = temp;
}
void heapify(vector<int> &hT, int i)
{
  int size = hT.size();
  int largest = i;
  int l = 2 * i + 1;
  int r = 2 * i + 2;
  if (l < size && hT[l] > hT[largest])
    largest = l;
  if (r < size && hT[r] > hT[largest])
    largest = r;

  if (largest != i)
  {
    swap(&hT[i], &hT[largest]);
    heapify(hT, largest);
  }
}
void insert(vector<int> &hT, int newNum)
{
  int size = hT.size();
  if (size == 0)
  {
    hT.push_back(newNum);
  }
  else
  {
    hT.push_back(newNum);
    for (int i = size / 2 - 1; i >= 0; i--)
    {
      heapify(hT, i);
    }
  }
}
void deleteNode(vector<int> &hT, int num)
{
  int size = hT.size();
  int i;
  for (i = 0; i < size; i++)
  {
    if (num == hT[i])
      break;
  }
  swap(&hT[i], &hT[size - 1]);

  hT.pop_back();
  for (int i = size / 2 - 1; i >= 0; i--)
  {
    heapify(hT, i);
  }
}
void printArray(vector<int> &hT)
{
  for (int i = 0; i < hT.size(); ++i)
    cout << hT[i] << " ";
  cout << "\n";
}

int main()
{
  vector<int> heapTree;

  insert(heapTree, 3);
  insert(heapTree, 4);
  insert(heapTree, 9);
  insert(heapTree, 5);
  insert(heapTree, 2);

  cout << "Max-Heap array: ";
  printArray(heapTree);

  deleteNode(heapTree, 4);

  cout << "After deleting an element: ";

  printArray(heapTree);
}

堆数据结构应用

• 在实现优先队列时使用堆。
• Dijkstra 算法
• 堆排序